Topics
Number System(Consolidating the Sense of Numberness)
Number System
Estimation
Ratio and Proportion
Algebra
Numbers in India and International System (With Comparison)
Geometry
Place Value
Mensuration
Natural Numbers and Whole Numbers (Including Patterns)
Data Handling
Negative Numbers and Integers
Number Line
HCF and LCM
Playing with Numbers
- Simplification of Brackets
- Finding Factors Using Rectangular Arrangements and Division
- Factors and Common Factors
- Multiples and Common Multiples
- Concept of Even and Odd Number
- Tests for Divisibility of Numbers
- Divisibility by 2
- Divisibility by 4
- Divisibility by 8
- Divisibility by 3
- Divisibility by 6
- Divisibility by 9
- Divisibility by 5
- Divisibility by 11
Sets
Ratio
Proportion (Including Word Problems)
Unitary Method
Fractions
- Concept of Fraction
- Types of Fractions
- Concept of Proper and Improper Fractions
- Concept of Mixed Fractions
- Like and Unlike Fraction
- Concept of Equivalent Fractions
- Conversion between Improper and Mixed fraction
- Conversion between Unlike and Like Fractions
- Simplest Form of a Fractions
- Comparing Fractions
- Addition of Fraction
- Subtraction of Fraction
- Multiplication of Fraction
- Division of Fractions
- Using Operator 'Of' with Multiplication and Division
- BODMAS Rule
- Problems Based on Fraction
Decimal Fractions
Percent (Percentage)
Idea of Speed, Distance and Time
Fundamental Concepts
Fundamental Operations (Related to Algebraic Expressions)
Substitution (Including Use of Brackets as Grouping Symbols)
Framing Algebraic Expressions (Including Evaluation)
Simple (Linear) Equations (Including Word Problems)
Fundamental Concepts
Angles (With Their Types)
Properties of Angles and Lines (Including Parallel Lines)
Triangles (Including Types, Properties and Constructions)
Quadrilateral
Polygons
The Circle
Symmetry (Including Constructions on Symmetry)
Recognition of Solids
Perimeter and Area of Plane Figures
Data Handling (Including Pictograph and Bar Graph)
Mean and Median
- Introduction
- Units of Measurement
- Measuring with a Protractor
- Steps to Measure an Angle Using a Protractor
- Activity: Make Your Own Paper Protractor
- Key Points Summary
- Common Errors
Introduction
-
An angle is formed when two rays meet at a point (called the vertex).
-
Angles are measured in degrees (°).
-
One full rotation = 360°.
- Tools like the protractor help us measure angles easily and accurately.
Why 360° in a Circle?
-
Ancient civilisations used 360° due to astronomy and calendars.
-
360 is divisible by many numbers: 2, 3, 4, 5, 6, 8, 9, 10, 12…
-
It makes calculations easier.
Units of Measurement
| Unit | Symbol | Conversion |
|---|---|---|
| Degree | ° | Basic unit |
| Minute | ′ | 1° = 60′ |
| Second | ″ | 1′ = 60″ |
Example:
(i) 32° 23' 15" and 49° 17' 32"
32° 23' 15"
+49° 17' 32"
81° 40' 47"
(ii) 74° 35' 18" and 9° 20' 53"
74° 35' 18"
+ 9° 20' 53"
83° 56' 11 "
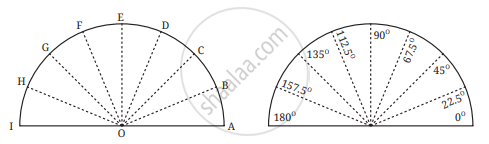
Measuring with a Protractor
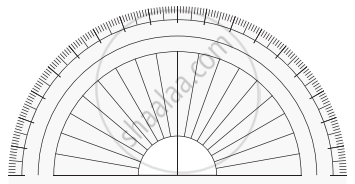
1. Unlabelled Protractor
-
Shows lines at 1° intervals but no numbers.
-
Used to explain the concept of dividing the semicircle.
2. Labelled Protractor
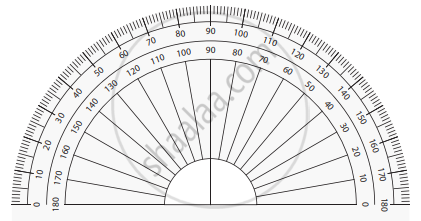
-
Found in your geometry box.
-
Has two number scales:
-
Inner scale: If your 0° is on the RIGHT
-
Outer scale: If your 0° is on the LEFT
-
Steps to Measure an Angle Using a Protractor
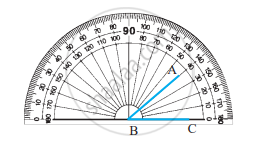
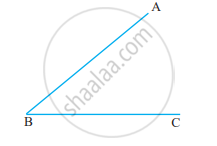
Measuring an Angle ∠ABC
- Positioning the Protractor:
Place the protractor so that the midpoint of its straight edge aligns with the vertex B of the angle. - Aligning the Base Ray:
Adjust the protractor so that ray BC coincides with the straight edge of the protractor. - Choosing the Correct Scale:
Identify the appropriate scale on the protractor, ensuring that the 0° mark aligns with ray BC. - Reading the Angle Measure:
Observe the point where ray BA intersects the curved edge of the protractor, indicating the degree measure of the angle.
Thus, the angle is recorded as m∠ABC = 40°, or simply ∠ABC = 40°.
Activity: Make Your Own Paper Protractor
steps:
-
Draw a circle on paper using any round object (like a cup or lid) and cut it out.
-
Fold the circle in half to make a semicircle.
-
Fold it again to make a quarter circle.
-
Fold it once more to get smaller sections.
-
Unfold and label the creases as 0°, 45°, 90°, 135°, and 180°.
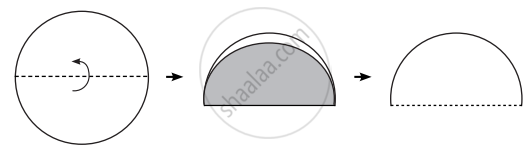
Observations:
-
Each fold divides the circle into equal angles.
-
The more you fold, the more angle marks you get.
-
The top of the first fold is always 90°.
-
You can see and feel how angles are created.
Conclusion:
-
A circle has 360°.
-
Folding helps divide the circle into standard angle measures.
-
You can estimate and understand angles better by making your own protractor!
Key Points Summary
-
1 full rotation = 360°
-
Right angle = 90°
-
Straight angle = 180°
-
Use correct scale on the protractor
-
Align properly: center on vertex, arm on baseline
Common Errors
-
Place the centre of the protractor away from the vertex.
-
Use the wrong scale (read inside when outside is needed).
-
Read the number before aligning the arm to 0° baseline.
-
Forget to extend angle arms to reach the protractor edge.
Test Yourself
Related QuestionsVIEW ALL [28]
Which angle has a large measure? First estimate and then measure.
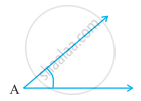 |
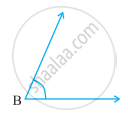 |
Measure of Angle A =
Measure of Angle B =
Measure and classify each angle :

|
Angle |
Measure |
Type |
|
∠AOB |
|
|
|
∠AOC |
|
|
|
∠BOC |
|
|
|
∠DOC |
|
|
|
∠DOA |
|
|
|
∠DOB |
|
|





