Topics
Integers
- Natural Numbers
- Whole Numbers
- Negative and Positive Numbers
- Integers
- Representation of Integers on the Number Line
- Ordering of Integers
- Addition of Integers
- Subtraction of Integers
- Properties of Addition and Subtraction of Integers
- Multiplication of a Positive and a Negative Integers
- Multiplication of Two Negative Integers
- Product of Three Or More Negative Integers
- Closure Property of Multiplication of Integers
- Commutative Property of Multiplication of Integers
- Multiplication of Integers with Zero
- Multiplicative Identity of Integers
- Associative Property of Multiplication of Integers
- Distributive Property of Multiplication of Integers
- Making Multiplication Easier of Integers
- Division of Integers
- Properties of Division of Integers
Fractions and Decimals
- Concept of Fraction
- Types of Fractions
- Concept of Proper and Improper Fractions
- Concept of Mixed Fractions
- Concept of Equivalent Fractions
- Like and Unlike Fraction
- Comparing Fractions
- Addition of Fraction
- Subtraction of Fraction
- Multiplication of a Fraction by a Whole Number
- Using Operator 'Of' with Multiplication and Division
- Multiplication of Fraction
- Division of Fractions
- Concept of Reciprocals or Multiplicative Inverses
- Problems Based on Fraction
- The Decimal Number System
- Comparing Decimal Numbers
- Addition of Decimal Fraction
- Subtraction of Decimal Numbers
- Multiplication of Decimal Numbers
- Division of Decimal Numbers
- Problems Based on Decimal Numbers
Data Handling
Simple Equations
Lines and Angles
The Triangle and Its Properties
- Basic Concepts of Triangles
- Classification of Triangles based on Sides
- Classification of Triangles based on Angles
- Median of a Triangle
- Altitudes of a Triangle
- Exterior Angle of a Triangle and Its Property
- Some Special Types of Triangles - Equilateral and Isosceles Triangles
- Basic Properties of a Triangle
- Right-angled Triangles and Pythagoras Property
Comparing Quantities
- Ratio
- Concept of Equivalent Ratios
- Proportion
- Unitary Method
- Basic Concept of Percentage
- Estimation in Percentages
- Interpreting Percentages
- Conversion between Percentage and Fraction or Decimal
- Ratios to Percents
- Increase Or Decrease as Percent
- Basic Concepts of Profit and Loss
- Profit or Loss as a Percentage
- Calculation of Interest
Congruence of Triangles
- Similarity and Congruency of Figures
- Congruence Among Line Segments
- Congruence of Angles
- Congruence of Triangles
- Criteria for Congruence of Triangles
- Criteria for Similarity of Triangles
- SAS Congruence Criterion
- ASA Congruence Criterion
- RHS Congruence Criterion
- Exceptional Criteria for Congruence of Triangles
Rational Numbers
- Rational Numbers
- Equivalent Rational Number
- Positive and Negative Rational Numbers
- Rational Numbers on a Number Line
- Rational Numbers in Standard Form
- Comparison of Rational Numbers
- Rational Numbers Between Two Rational Numbers
- Addition of Rational Number
- Subtraction of Rational Number
- Multiplication of Rational Numbers
- Division of Rational Numbers
Perimeter and Area
- Basic Concepts in Mensuration
- Concept of Perimeter
- Perimeter of a Rectangle
- Perimeter of Squares
- Perimeter of Triangle
- Perimeter of Polygon
- Concept of Area
- Area of Square
- Area of Rectangle
- Triangles as Parts of Rectangles and Square
- Generalising for Other Congruent Parts of Rectangles
- Area of a Parallelogram
- Area of a Triangle
- Circumference of a Circle
- Area of Circle
- Conversion of Units
- Problems based on Perimeter
- Problems based on Area
Practical Geometry
- Construction of a Line Parallel to a Given Line, Through a Point Not on the Line
- Construction of Triangles
- Constructing a Triangle When the Length of Its Three Sides Are Known (SSS Criterion)
- Constructing a Triangle When the Lengths of Two Sides and the Measure of the Angle Between Them Are Known. (SAS Criterion)
- Constructing a Triangle When the Measures of Two of Its Angles and the Length of the Side Included Between Them is Given. (ASA Criterion)
- Constructing a Right-angled Triangle When the Length of One Leg and Its Hypotenuse Are Given (RHS Criterion)
Algebraic Expressions
Exponents and Powers
- Concept of Exponents
- Multiplying Powers with the Same Base
- Dividing Powers with the Same Base
- Taking Power of a Power
- Multiplying Powers with Different Base and Same Exponents
- Dividing Powers with Different Base and Same Exponents
- Numbers with Exponent Zero, One, Negative Exponents
- Miscellaneous Examples Using the Laws of Exponents
- Decimal Number System Using Exponents and Powers
- Crores
Symmetry
Visualizing Solid Shapes
- Introduction
- Case 1: Comparing Like Fractions
- Case 2: Comparing Unlike Fractions
- Case 3: Comparing Unlike Fractions with the Same Numerators
- Example 1
- Example 2
- Key Points Summary
Introduction
Fractions show parts of a whole. Sometimes, we need to decide who ate more pizza, which bottle has more water, or which team scored a bigger part of the total points. To do this, we compare fractions—just like comparing slices of a cake!
Comparing fractions means finding which is greater or smaller, or if they are equal. The method depends on whether they have the same denominator, the same numerator, or neither.
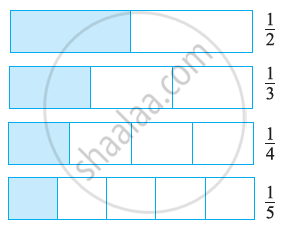
By looking at the shading:
`1/2` > `1/3` > `1/4` > `1/5`
As the denominator increases (while the numerator remains 1), the fraction decreases.
Case 1: Comparing Like Fractions
Fractions with the same denominator are called like fractions.
Rule:
The fraction with the greater numerator is greater.
Example:
Let us compare: `3/8 and 5/8`.

- Both have a denominator of 8.
- 3 < 5.
- `3/8 < 5/8`
Case 2: Comparing Unlike Fractions
Method 1: Make Denominators Equal
- Find the LCM of the denominators.
- Convert each fraction to an equivalent fraction with this common denominator.
- Compare the numerators.
Example:
Compare `8/15 and 12/25`.
- L.C.M. of denominators 15 and 25 = 75,
∴ `8/ 15` = `"8 × 5"/ "15 × 5"` = ` 40/ 75` and
`12 / 25` = `"12 × 3"/ "25 × 3"` = ` 36 / 75` - 40 > 36.
Hence, ` 36 / 75` i.e., `12 / 25` is smaller.
Method 2: Make Numerators Equal
- Find the LCM of the numerators.
- Convert fractions to equivalent fractions with this common numerator.
- Compare the denominators. The smaller denominator gives the greater fraction.
Example:
Compare `8/15 and 12/25`.
- The L.C.M. of numerators 8 and 12 is 24.
∴ `8/ 15` = `"8 × 3"/ "15 × 3"` = ` 24/ 45` and
`12 / 25` = `"12 × 2"/ "25 × 2"` = ` 24 / 50` - 45 > 50
Hence, ` 24 / 50` i.e., `12 / 25` is smaller.
Case 3: Comparing Unlike Fractions with the Same Numerators
For fractions with the same numerator, the fraction with the smaller denominator is larger.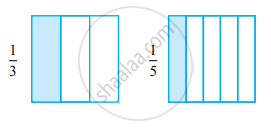
- `1/3` divides the whole into 3 parts; `1/5` divides it into 5 parts.
- Hence, `1/3 > 1/5`.
Example 1
Compare the fractions `2 / 3`, `3/4`, `5/12`, and `9/16` by writing them in descending order.
Solution:
Make Denominators Equal
- The L.C.M. of the denominators 3, 4, 12 and 16 is 48.
`2 / 3` = `"2 × 16" / "3 × 16"` = `32/48`
`3/4` = `"3 × 12" / "4 × 12"` = `36/48`
`5/12` = `"5 × 4" / "12 × 4"` = `20/48`
`9/16` = `"9 × 3" / "16 × 3"` = `27/48` - Compare Numerator: 36 > 32 > 27 > 20
- Descending order: `3/4` > `2 / 3` > `9/16` > `5/12`
Alternative method: Equal Numerator
- The L.C.M. of the numerators 2, 3, 5 and 9 = 90
`2 / 3` = `"2 × 45" / "3 × 45"` = `90/135`
`3/4` = `"3 × 30" / "4 × 30"` = `90/120`
`5/12` = `"5 × 18" / "12 × 18"` = `90/216`
`9/16` = `"9 × 10" / "16 × 10"` = `90/160` - smallest denominator ⇒ biggest fraction
largest denominator ⇒ smallest fraction. - Compare denominators: 120 < 135 < 160 < 216.
- Descending order: `3/4` > `2 / 3` > `9/16` > `5/12`
Example 2
Compare `4/5` and `7/9`
- Make denominators the same.
- LCM of 5 and 9 = 45.
`"4 × 9"/ "5 × 9"` = `36/ 45`
`7/9` = `"7 × 5"/"9 × 5"` = `35/45`
Clearly, `36/ 45` > `35/45`
So, `4/5` > `7/9`
Key Points Summary
-
Like denominators: bigger numerator wins.
-
Unlike denominators: convert to like denominators.
-
Same numerators: smaller denominator wins.
Example Question 1
Find answers to the following. Write and indicate how you solved them.
Is `5/9` equal to `4/5`?
`5/9, 4/5`
Converting these into like fractions,
`5/9 = 5/9 xx 5/5 = 25/45`
`4/5 = 4/5 xx 9/9 = 36/45`
As, `36/45 ≠ 25/45`,
Therefore, `5/9 "is not equal to" 4/5`.
Example Question 2
Find answers to the following. Write and indicate how you solved them.
Is `9/16` equal to `5/9`?
`9/16, 5/9`
Converting these into like fractions,
`9/16 = 9/16 xx 9/9 = 81/144`
`5/9 = 5/9 xx 16/16 = 80/144`
As, `81/144 ≠ 80/144`,
Therefore, `9/16 "is not equal to" 5/9`.
Example Question 3
Find answers to the following. Write and indicate how you solved them.
Is `4/5` equal to `16/20`?
`4/5, 16/20`
`16/20 = (4 xx 4)/(5 xx 4) = 4/5`
Therefore, `4/5 = 16/20`.
Example Question 4
Ila read 25 pages of a book containing 100 pages. Lalita read `2/5` of the same book. Who reads less?
Numbers of pages read by Lalita = `2/5 xx 100` = 40
Number of pages read by Ila = 25
Hence, Ila has read less number of pages.
Example Question 5
Asha and Samuel have bookshelves of the same size partly filled with books. Asha’s shelf is `5/6`th full and Samuel’s shelf is `2/5`th full. Whose bookshelf is more full? By what fraction?
Fraction of Asha’s shelf = `5/6`
Fraction of Samuel’s shelf = `2/5`
Converting these into like fractions,
`5/6 = 5/6 xx 5/5 = 25/30`
`2/5 = 2/5 xx 6/6 = 12/30`
`25/30 > 12/30`
Clearly, Asha’s bookshelf is more full.
Difference = `5/6 - 2/5 = 25/30 - 12/30 = 13/30`.
Example Question 6
Jaidev takes `2 1/5` minutes to walk across the school ground. Rahul takes `7/4` minutes to do the same. Who takes less time and by what fraction?
Time taken by Jaidev = `2 1/5 "minutes" = 11/5` min
Time taken by Rahul = `7/4` min
Converting these into like fractions,
`11/5 = 11/5 xx 4/4 = 44/20`
`7/4 = 7/4 xx 5/5 = 35/20`
As 44 > 35,
`11/5 > 7/4`
Hence, Rahul takes lesser time.
Difference = `11/5 - 7/4`
= `44/20 - 35/20 = 9/20` min.
Test Yourself
Shaalaa.com | Comparison Of Like Fractions
Series: Comparing Fractions
00:09:30 undefined
00:11:20 undefined
00:10:59 undefined
00:10:56 undefined
00:09:42 undefined
00:07:40 undefined
00:07:25 undefined
