Topics
Integers
- Concept for Natural Numbers
- Concept for Whole Numbers
- Negative and Positive Numbers
- Concept of Integers
- Representation of Integers on the Number Line
- Concept for Ordering of Integers
- Addition of Integers
- Subtraction of Integers
- Properties of Addition and Subtraction of Integers
- Multiplication of a Positive and a Negative Integers
- Multiplication of Two Negative Integers
- Product of Three Or More Negative Integers
- Closure Property of Multiplication of Integers
- Commutative Property of Multiplication of Integers
- Multiplication of Integers with Zero
- Multiplicative Identity of Integers
- Associative Property of Multiplication of Integers
- Distributive Property of Multiplication of Integers
- Making Multiplication Easier of Integers
- Division of Integers
- Properties of Division of Integers
Fractions and Decimals
- Concept of Fractions
- Fraction and its Types
- Concept of Proper Fractions
- Improper Fraction and Mixed Fraction
- Concept of Equivalent Fractions
- Like and Unlike Fraction
- Comparing Fractions
- Addition of Fraction
- Subtraction of Fraction
- Multiplication of a Fraction by a Whole Number
- Fraction as an Operator 'Of'
- Multiplication of Fraction
- Division of Fractions
- Concept of Reciprocal or Multiplicative Inverse
- Problems Based on Fraction
- The Decimal Number System
- Comparing Decimal Numbers
- Addition of Decimal Fraction
- Subtraction of Decimal Numbers
- Multiplication of Decimal Fractions
- Multiplication of Decimal Numbers by 10, 100 and 1000
- Division of Decimal Numbers by 10, 100 and 1000
- Division of Decimal Fractions
- Division of a Decimal Number by Another Decimal Number
- Problems Based on Decimal Numbers
Data Handling
Simple Equations
Lines and Angles
- Concept of Points
- Concept of Line
- Concept of Line Segment
- Concept of Angle
- Complementary Angles
- Supplementary Angles
- Concept of Angle
- Concept of Linear Pair
- Concept of Vertically Opposite Angles
- Concept of Intersecting Lines
- Introduction to Parallel Lines
- Pairs of Lines - Transversal
- Pairs of Lines - Angles Made by a Transversal
- Pairs of Lines - Transversal of Parallel Lines
The Triangle and Its Properties
- Concept of Triangles
- Classification of Triangles (On the Basis of Sides, and of Angles)
- Classification of Triangles based on Sides- Equilateral, Isosceles, Scalene
- Classification of Triangles based on Sides- Equilateral, Isosceles, Scalene
- 3. Classification of Triangles based on Angles: Acute-Angled, Right-Angled, Obtuse-Angled
- 3. Classification of Triangles based on Angles: Acute-Angled, Right-Angled, Obtuse-Angled
- Median of a Triangle
- Altitudes of a Triangle
- Exterior Angle of a Triangle and Its Property
- Angle Sum Property of a Triangle
- Some Special Types of Triangles - Equilateral and Isosceles Triangles
- Sum of the Lengths of Two Sides of a Triangle
- Right-angled Triangles and Pythagoras Property
Comparing Quantities
- Concept of Ratio
- Concept of Equivalent Ratios
- Concept of Proportion
- Concept of Unitary Method
- Basic Concept of Percentage
- Conversion between Percentage and Fraction
- Converting Decimals to Percentage
- Conversion between Percentage and Fraction
- Converting Percentages to Decimals
- Estimation in Percentages
- Interpreting Percentages
- Converting Percentages to “How Many”
- Ratios to Percents
- Increase Or Decrease as Percent
- Basic Concepts of Profit and Loss
- Profit or Loss as a Percentage
- Calculation of Interest
Congruence of Triangles
Rational Numbers
- Rational Numbers
- Equivalent Rational Number
- Positive and Negative Rational Numbers
- Rational Numbers on a Number Line
- Rational Numbers in Standard Form
- Comparison of Rational Numbers
- Rational Numbers Between Two Rational Numbers
- Addition of Rational Number
- Subtraction of Rational Number
- Multiplication of Rational Numbers
- Division of Rational Numbers
Perimeter and Area
- Mensuration
- Concept of Perimeter
- Perimeter of a Rectangle
- Perimeter of Squares
- Perimeter of Triangles
- Perimeter of Polygon
- Concept of Area
- Area of Square
- Area of Rectangle
- Triangles as Parts of Rectangles and Square
- Generalising for Other Congruent Parts of Rectangles
- Area of a Parallelogram
- Area of a Triangle
- Circumference of a Circle
- Area of Circle
- Conversion of Units
- Problems based on Perimeter and Area
Algebraic Expressions
- Algebraic Expressions
- Terms, Factors and Coefficients of Expression
- Like and Unlike Terms
- Types of Algebraic Expressions as Monomials, Binomials, Trinomials, and Polynomials
- Addition of Algebraic Expressions
- Subtraction of Algebraic Expressions
- Evaluation of Algebraic Expressions by Substituting a Value for the Variable.
- Use of Variables in Common Rules
Practical Geometry
- Construction of a Line Parallel to a Given Line, Through a Point Not on the Line
- Construction of Triangles
- Constructing a Triangle When the Length of Its Three Sides Are Known (SSS Criterion)
- Constructing a Triangle When the Lengths of Two Sides and the Measure of the Angle Between Them Are Known. (SAS Criterion)
- Constructing a Triangle When the Measures of Two of Its Angles and the Length of the Side Included Between Them is Given. (ASA Criterion)
- Constructing a Right-angled Triangle When the Length of One Leg and Its Hypotenuse Are Given (RHS Criterion)
Exponents and Powers
- Concept of Exponents
- Multiplying Powers with the Same Base
- Dividing Powers with the Same Base
- Taking Power of a Power
- Multiplying Powers with Different Base and Same Exponents
- Dividing Powers with Different Base and Same Exponents
- Numbers with Exponent Zero, One, Negative Exponents
- Miscellaneous Examples Using the Laws of Exponents
- Decimal Number System Using Exponents and Powers
- Crores
Symmetry
Visualizing Solid Shapes
Definition
SAS Congruence criterion: If under a correspondence, two sides and the angle included between them of a triangle are equal to two corresponding sides and the angle included between them of another triangle, then the triangles are congruent.
Notes
SAS Congruence criterion:
If under a correspondence, two sides and the angle included between them of a triangle are equal to two corresponding sides and the angle included between them of another triangle, then the triangles are congruent.
Which congruence criterion do you use in the following?
Given:
ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ∆PQR ≅ ∆XYZ
Solution: SAS Congruence criterion, as two sides and the angle included between these sides of ΔPQR are equal to two sides and the angle included between these sides of ΔXYZ.
Example
Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by using the SAS congruence rule. If the triangles are congruent, write them in symbolic form.
∆ABC, AB = 7 cm, BC = 5 cm, ∠B = 50°.
∆DEF, DE = 5 cm, EF = 7 cm, ∠E = 50°.
Here,
AB = EF ( = 7 cm),
BC = DE ( = 5 cm) and
included ∠B = included ∠E ( = 50°).
Also, A ↔ F B ↔ E and C ↔ D.
Therefore, ∆ABC ≅ ∆FED................(By SAS congruence rule).
Example
Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by using the SAS congruence rule. If the triangles are congruent, write them in symbolic form.
∆ABC, AB = 4.5 cm, AC = 4 cm, ∠A = 60°.
∆DEF, DE = 4 cm, FD = 4.5 cm, ∠D = 55°.
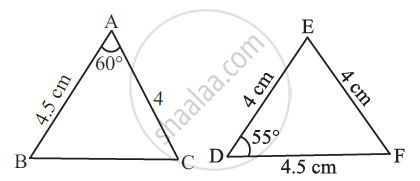
Here, AB = FD and AC = DE.
But included ∠A ≠ included ∠D.
So, we cannot say that the triangles are congruent.
Example
In Fig,
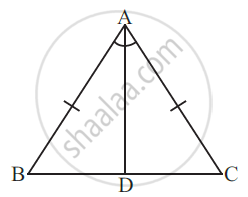
AB = AC and AD is the bisector of ∠BAC.
(i) State three pairs of equal parts in triangles ADB and ADC.
(ii) Is ∆ADB ≅ ∆ADC? Give reasons.
(iii) Is ∠B = ∠C? Give reasons.
(i) The three pairs of equal parts are as follows:
AB = AC...................(Given)
∠BAD = ∠CAD......(AD bisects ∠BAC) and
AD = AD..................(common)
(ii) Yes, ∆ADB ≅ ∆ADC.....(By SAS congruence rule)
(iii) ∠B = ∠C.........................(Corresponding parts of congruent triangles)
