Topics
Integers
- Natural Numbers
- Whole Numbers
- Negative and Positive Numbers
- Integers
- Representation of Integers on the Number Line
- Ordering of Integers
- Addition of Integers
- Subtraction of Integers
- Properties of Addition and Subtraction of Integers
- Multiplication of a Positive and a Negative Integers
- Multiplication of Two Negative Integers
- Product of Three Or More Negative Integers
- Closure Property of Multiplication of Integers
- Commutative Property of Multiplication of Integers
- Multiplication of Integers with Zero
- Multiplicative Identity of Integers
- Associative Property of Multiplication of Integers
- Distributive Property of Multiplication of Integers
- Making Multiplication Easier of Integers
- Division of Integers
- Properties of Division of Integers
Fractions and Decimals
- Concept of Fraction
- Types of Fractions
- Concept of Proper and Improper Fractions
- Concept of Mixed Fractions
- Concept of Equivalent Fractions
- Like and Unlike Fraction
- Comparing Fractions
- Addition of Fraction
- Subtraction of Fraction
- Multiplication of a Fraction by a Whole Number
- Using Operator 'Of' with Multiplication and Division
- Multiplication of Fraction
- Division of Fractions
- Concept of Reciprocals or Multiplicative Inverses
- Problems Based on Fraction
- The Decimal Number System
- Comparing Decimal Numbers
- Addition of Decimal Fraction
- Subtraction of Decimal Numbers
- Multiplication of Decimal Numbers
- Division of Decimal Numbers
- Problems Based on Decimal Numbers
Data Handling
Simple Equations
Lines and Angles
The Triangle and Its Properties
- Basic Concepts of Triangles
- Classification of Triangles based on Sides
- Classification of Triangles based on Angles
- Median of a Triangle
- Altitudes of a Triangle
- Exterior Angle of a Triangle and Its Property
- Some Special Types of Triangles - Equilateral and Isosceles Triangles
- Basic Properties of a Triangle
- Right-angled Triangles and Pythagoras Property
Comparing Quantities
- Ratio
- Concept of Equivalent Ratios
- Proportion
- Unitary Method
- Basic Concept of Percentage
- Estimation in Percentages
- Interpreting Percentages
- Conversion between Percentage and Fraction or Decimal
- Ratios to Percents
- Increase Or Decrease as Percent
- Basic Concepts of Profit and Loss
- Profit or Loss as a Percentage
- Calculation of Interest
Congruence of Triangles
- Similarity and Congruency of Figures
- Congruence Among Line Segments
- Congruence of Angles
- Congruence of Triangles
- Criteria for Congruence of Triangles
- Criteria for Similarity of Triangles
- SAS Congruence Criterion
- ASA Congruence Criterion
- RHS Congruence Criterion
- Exceptional Criteria for Congruence of Triangles
Rational Numbers
- Rational Numbers
- Equivalent Rational Number
- Positive and Negative Rational Numbers
- Rational Numbers on a Number Line
- Rational Numbers in Standard Form
- Comparison of Rational Numbers
- Rational Numbers Between Two Rational Numbers
- Addition of Rational Number
- Subtraction of Rational Number
- Multiplication of Rational Numbers
- Division of Rational Numbers
Perimeter and Area
- Basic Concepts in Mensuration
- Concept of Perimeter
- Perimeter of a Rectangle
- Perimeter of Squares
- Perimeter of Triangle
- Perimeter of Polygon
- Concept of Area
- Area of Square
- Area of Rectangle
- Triangles as Parts of Rectangles and Square
- Generalising for Other Congruent Parts of Rectangles
- Area of a Parallelogram
- Area of a Triangle
- Circumference of a Circle
- Area of Circle
- Conversion of Units
- Problems based on Perimeter
- Problems based on Area
Practical Geometry
- Construction of a Line Parallel to a Given Line, Through a Point Not on the Line
- Construction of Triangles
- Constructing a Triangle When the Length of Its Three Sides Are Known (SSS Criterion)
- Constructing a Triangle When the Lengths of Two Sides and the Measure of the Angle Between Them Are Known. (SAS Criterion)
- Constructing a Triangle When the Measures of Two of Its Angles and the Length of the Side Included Between Them is Given. (ASA Criterion)
- Constructing a Right-angled Triangle When the Length of One Leg and Its Hypotenuse Are Given (RHS Criterion)
Algebraic Expressions
Exponents and Powers
- Concept of Exponents
- Multiplying Powers with the Same Base
- Dividing Powers with the Same Base
- Taking Power of a Power
- Multiplying Powers with Different Base and Same Exponents
- Dividing Powers with Different Base and Same Exponents
- Numbers with Exponent Zero, One, Negative Exponents
- Miscellaneous Examples Using the Laws of Exponents
- Decimal Number System Using Exponents and Powers
- Crores
Symmetry
Visualizing Solid Shapes
Notes
Concept of Rotational Symmetry:
-
Rotation turns an object about a fixed point.
-
Rotation, like the movement of the hands of a clock, is called a clockwise rotation; otherwise, it is said to be anticlockwise.
-
When an object rotates, its shape and size do not change.
-
The rotation turns an object about a fixed point. This fixed point is the centre of rotation.
-
The angle of turning during rotation is called the angle of rotation.
-
A full turn, you know, means a rotation of 360°.
-
A half-turn means rotation by 180°; a quarter-turn is a rotation by 90°.
-
If, after a rotation, an object looks exactly the same, we say that it has rotational symmetry.
-
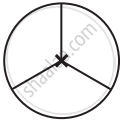
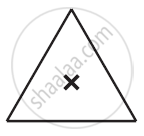
In a complete turn (of 360 degrees), the number of times an object looks exactly the same is called the order of rotational symmetry. The order of symmetry of a square, for example, is 4 while, for an equilateral triangle, it is 3.
Rotation turns an object about a fixed point.
Rotation, like the movement of the hands of a clock, is called a clockwise rotation; otherwise, it is said to be anticlockwise.
When an object rotates, its shape and size do not change.
The rotation turns an object about a fixed point. This fixed point is the centre of rotation.
The angle of turning during rotation is called the angle of rotation.
A full turn, you know, means a rotation of 360°.
A half-turn means rotation by 180°; a quarter-turn is a rotation by 90°.
If, after a rotation, an object looks exactly the same, we say that it has rotational symmetry.
In a complete turn (of 360 degrees), the number of times an object looks exactly the same is called the order of rotational symmetry. The order of symmetry of a square, for example, is 4 while, for an equilateral triangle, it is 3.
For Example:

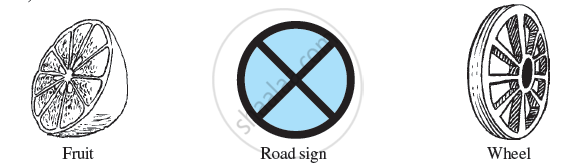
The Paper windmill in the picture looks symmetrical, but you do not find any line of symmetry. No folding can help you to have coincident halves. However, if you rotate it by 90° about the fixed point, the windmill will look exactly the same. We say the windmill has rotational symmetry. In a full turn, there are precisely four positions (on rotation through the angles 90°,180°, 270°, and 360°) when the windmill looks exactly the same. Because of this, we say it has rotational symmetry of order 4.
The point where we have the pin is the centre of rotation. It is the intersecting point of the diagonals in this case. Every object has rotational symmetry of order 1, as it occupies the same position after a rotation of 360° (i.e., one complete revolution). Such cases have no interest for us.
For example, when you slice certain fruits, the cross-sections are shapes with rotational symmetry.
Shaalaa.com | What is Rotational Symmetry?
Related QuestionsVIEW ALL [65]
For the following picture, find the number of lines of symmetry and also find the order of rotation.
For the following picture, find the number of lines of symmetry and also find the order of rotation.